感谢 Vitalik Buterin 和 Yahsin Huang 的审阅和反馈
触发警告:高中数学
在 eth2.0 分片中,验证者被随机分配到委员会中以生成跨链接。每个委员会必须至少有一个称为“最低委员会大小”的最小成员数。在 Eth2.0 规范 中,附注指出推荐的验证者数量是 111 个。选择了一个常量 TARGET_COMMITTEE_SIZE 为 128,作为 111 的近似数,因为规范中的每个常量都定义为 2 的幂。2 的幂更容易记忆和仅用人脑进行计算。
本文带你了解这个 111 魔法数字如何影响整个系统的安全性。
委员会的安全性是如何定义的。假设协议几乎拥有所有验证者的诚实多数,即,2/3 的诚实验证者 😇 和 1/3 的恶意验证者 😈,我们希望每个委员会在协议将这些验证者随机分配到委员会时仍然拥有诚实多数。
举个具体的例子,假设我们有 30 万个总验证者,其中有 10 万个是攻击者。该协议有 1024(1K)个委员会,每个委员会分配 300 个验证者。如果一个委员会不幸有 200 个攻击者,那么这个委员会就不安全。
这种情况类似于从箱子中抽球。假设有一个巨大的箱子,里面装有数百万个球,你恰好知道 2/3 的球是黄色的 😇,而 1/3 是紫色的 😈。我们想抽取 3 个球,并要求不超过 1 个为紫色。
我们可以用一些公式来分析“抽到 2 或 3 个紫色球”的事件概率。
- 对于“3 个紫色”的情况,概率为 (1/3) (1/3) (1/3) = 0.037
- 对于“2 个紫色和 1 个黄色”的情况,不要忘记 3 种可能的组合 (😈😈😇, 😈😇😈, 😇😈😈)。 (1/3) (1/3) (2/3) * choose(3, 1) = 0.222。
将上述步骤整理成一些 Python 函数之后,我们可以得出从抽球数量到不良结果概率的映射。
# 来源: https://vitalik.ca/files/Ithaca201807\_Sharding.pdf 页 11 deffac(n): return n * fac(n-1) ifnelse1 defchoose(n, k): returnfac(n) //fac(k) //fac(n-k) defprob(n, k, p): return p * * k * (1-p) * * (n-k) * choose(n, k) defprobgte(n, k, p): return sum(\[prob(n, i, p) foriinrange(k, n+1)\]) 查看原始代码
prob 给出了从 3 个球抽取中得到 2 个紫色 😈 的概率,而 probgte 给出了获取 2 个或更多紫色 😈 的概率(即 2 和 3)。这是将 k=2 和 n=3 作为函数参数传递的。
正如下图所示,随着抽取球的数量增加,概率降低。当 k 恰好是 n 的 2/3 时,出现锯齿状。
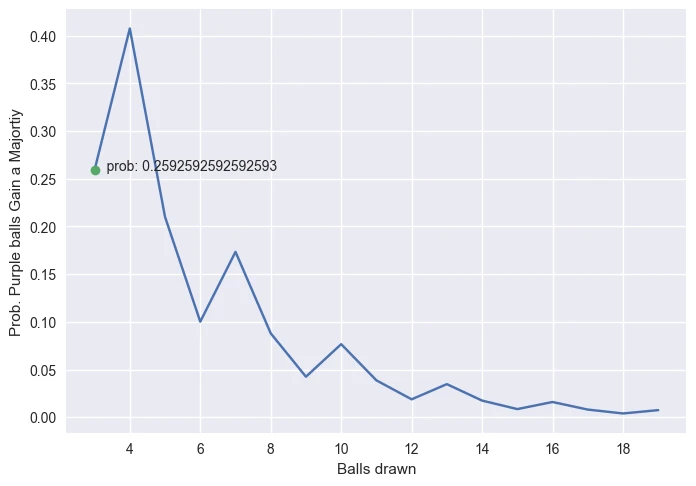
注意:在某些数据点上,我错误地将未通过 2/3 的概率包含在计算中。例如,在抽取 4 个球的情况下,2 个紫色的概率不应加上。我错误地使用 int 而不是 ceil 将 Python 中的分数转换成整数。
>>> list(range(int(4*2/3), 4+1 )) # 错误 [2, 3, 4] >>> list(range(ceil(4*2/3), 4+1 )) # 正确 [3, 4]感谢 Gusti Albrecht 指出图表中的错误!
如果你不相信,当数字较大时,趋势更显著。
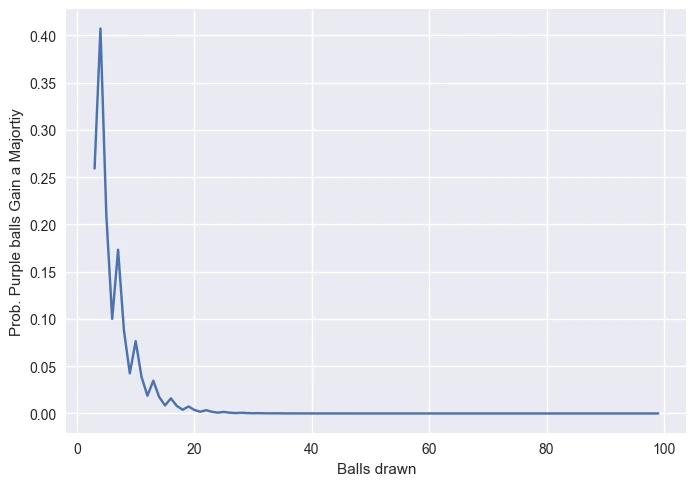
将上述事实翻译到委员会问题中,这意味着我们可以增加委员会的大小,以减少委员会中有 2/3 的攻击者的概率。通过指定一个我们可以接受的小概率,我们可以确定所需的最小委员会大小。
假设概率为 2 -40,委员会至少需要 111 名成员。
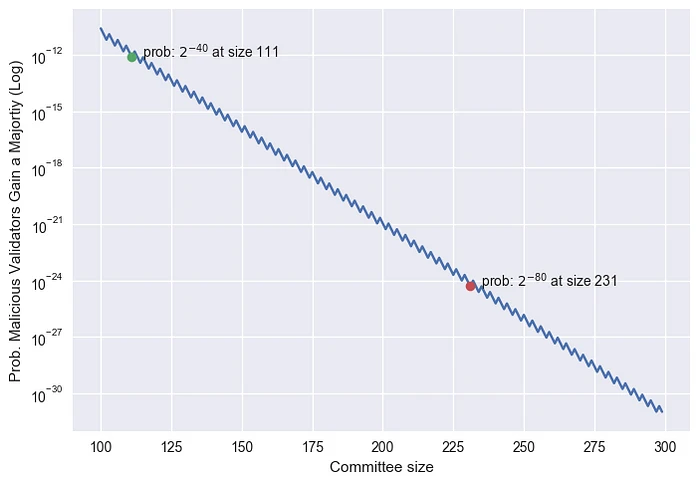
请注意,y 轴为对数比例
一些其他因素可能会影响这个委员会的大小。
- 如果攻击者操纵随机数生成器,选择更小的概率会更好,因此需要更大的委员会大小。40 位的操控意味着攻击者可以抽样 2 40 次,因此在这种情况下,我们将概率参数化为 2 -80,以针对 2 -40 的安全失败率。此时委员会大小为 231。
- 为了保持保守,可以目标指定 2/5 的恶意验证者不在某个委员会中占据 3/5。为了使该概率保持在 2 -40 以下,委员会大小现在为 315。
数学爱好者的总结
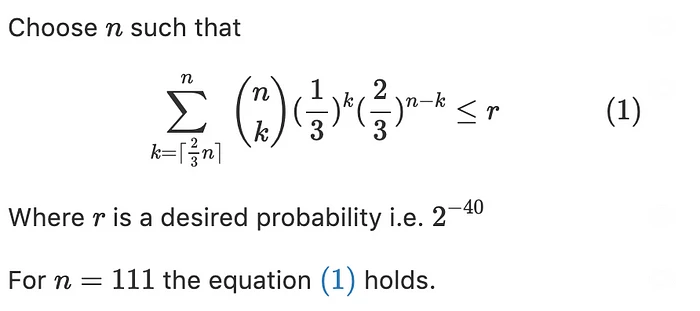
再次感谢 Gusti Albrecht 对此总结的贡献。
参考文献
- Eth2.0 规范
- Vitalik 在伊萨卡的演讲幻灯片,2018年7月 页 9–11
- Serenity 设计理由 Crosslink-committees 部分
- 请在 Proto 的图表 中查看洗牌是如何工作的
代码
x= \[\] y= \[\] lable\_1\_p=None foriinrange(3, 20): two\_third=int(i * 2/3) p=probgte(i, two\_third, 1/3) x.append(i) y.append(p) ifi==3: lable\_1\_p=p plt.plot(x, y) plt.plot(3, lable\_1\_p, 'o') plt.text(3, lable\_1\_p, r' prob: %s'%lable\_1\_p) plt.ylabel('Prob. 紫色球获得多数') plt.xlabel('抽取球数量') plt.show() 查看原始代码
x= \[\] y= \[\] foriinrange(3, 100): two\_third=int(i * 2/3) p=probgte(i, two\_third, 1/3) x.append(i) y.append(p) plt.ylabel('Prob. 紫色球获得多数') plt.xlabel('抽取球数量') plt.plot(x, y) plt.show() 查看原始代码
x= \[\] y= \[\] label\_1=None label\_2=None foriinrange(100, 300): two\_third=int(i * 2/3) p=probgte(i, two\_third, 1/3) x.append(i) y.append(p) ifp<2 * * -40andlabel\_1isNone: label\_1= (i, p) ifp<2 * * -80andlabel\_2isNone: label\_2= (i, p) plt.yscale('log') plt.plot(x, y) plt.plot( * label\_1, 'o') plt.text( * label\_1, r' prob: $2^{-40}$ at size %s'%label\_1\[0\]) plt.plot( * label\_2, 'o') plt.text( * label\_2, r' prob: $2^{-80}$ at size %s'%label\_2\[0\]) plt.ylabel('Prob. 恶意验证者获得多数 (对数)') plt.xlabel('委员会大小') plt.show() 查看原始代码
fromscipy.specialimportcomb defprob(n, k, p): return p * * k * (1-p) * * (n-k) * comb(n, k) defprobgte(n, k, p): return sum(\[prob(n, i, p) foriinrange(k, n+1)\]) 查看原始代码 ```
importmatplotlib.pyplotasplt plt.style.use('seaborn') 查看原始代码 ```
foriinrange(100, 350): majority=int(i * 3/5) p=probgte(i, majority, 2/5) ifp<2 * * -40: print(i) 查看原始代码
- 原文链接: medium.com/@chihchenglia...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~


